Helligkeit und Lichtberechnung

 

 

 

 

Logarithmische Lichtberechnung

 

 

Die Helligkeiten nehmen wir nicht linear wahr sondern logarithmisch.

Dafür gibt es zwei unterschiedliche Skalen: zur Basis von 10 und zur Basis von 2

 

In der Fotografie wird der Dynamikbereich in Lichtwerten ausgedrückt (LW, -engl. EV (Exposure Value)). Dieser beruht auf einer logarithmischen Skala zur Basis von 2 (also die Hochzahlen von 2): Jede Verdoppelung der Lichtmenge bedeutet eine Erhöhung des Lichtwertes um eine Stufe.

 

 

 

In der analogen Fotografie bezieht man sich auf die Belichtungseinheiten. Was bedeutet, dass sich bei einer Halbierung oder Verdoppelung des Lichts eine schließliche Schwärzung auf dem Negativ sichtbar wird.

 

 

 

 

 

Dagegen findet gerade bei Angaben des Dichteumfangs die Berechnung mir der logarithmischen Skala mit der Basis von 10 statt (also die Hochzahlen von 10).

Die Zahl 1 steht demnach für 10 (10 hoch 1), 2 für 100 (10²), 3 für 1000 (10³), usw.

Von einer Zahl zur nächsten, die um 1 größer ist, verzehnfacht sich die zunehmende Lichtmenge, bzw verzehnfacht sich die Dichte des Films, also die Schwärzung

 

 

 

Das ergibt sich aus folgender

Sensitometrischen Berechnung

 

D = log 1/T

(T steht für Transmission = Lichtdurchlässigkeit)

 

Beim Negativ ist das das Verhältnis der eingestrahlten und durchgelassenen Lichtmenge. Man bezeichnet dies als Opazität, die sich entgegengesetzt zur Transmission verhält. Z.B. bedeutet eine Lichtdurchlässigkeit von 10% eine Deckkraft von 90%.

 

 

 

 

 

 

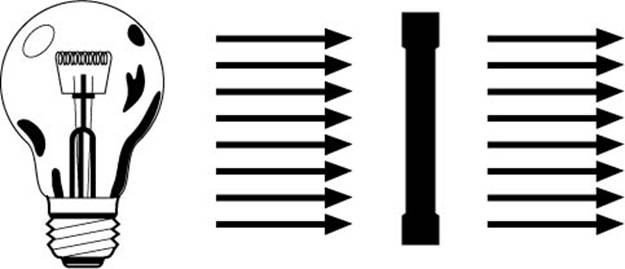
Bei einer Lichtmenge von 100% oder wenn das Negativ völlig transparent ist (Lichtdurchlässigkeit = 100%) beziehungsweise wenn das Licht mit voller Kraft strahlt ergibt sich folgende Formel.

 

D = log 1 = 0          oder

D = log 1/1,00 

 

Heißt bei vollkommener Transparenz weist das Negativ keine Dichte auf.

 

 

 

 

 

 

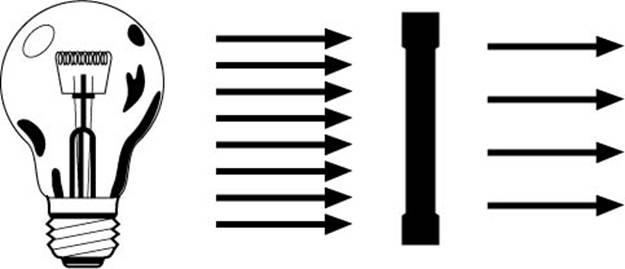
Minimiert man die Lichtmenge um die Hälfte oder wenn die Durchlässigkeit nur noch halb so stark ist, nämlich 50% gilt folgendes:

 

D = log 2 = 0,3  oder

D = log 1/0,50 = 0,3

 

 

 

 

 

 

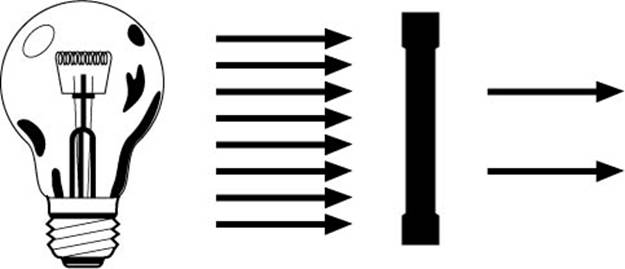
Bei noch einmal der Hälfte, bei Lichtdurchlässigkeit von 25% erhält man nach obiger Formel

 

D = log 4 = 0,3  oder

D = log 1/0,25 = 0,6

 

 

 

 

Daraus geht hervor, dass sich bei einer Verdoppelung oder Halbierung der Transmission ein Licht- oder Dichtezuwachs oder Verminderung jeweils um den Faktor 0,3 ergibt (arithmetische Progression = log 2). Dieser Faktor bestimmt die LW-Stufe und jeder Teilschritt der durch diesen Faktor erzeugt wird entspricht einem Blendenschritt/Belichtungsintervall.

den 10 hoch 0,3 ergibt 2.

 

 

 

D = log 1/0,10           oder

D = log 10 = 1

 

Wenn nur noch ein zehntel des Lichts (10%) durch das Negativ kommt, bedeutet das einen Dichtezuwachs von 1 oder einen Helligkeitsverminderung von der 10fachen Lichtmenge.

 

 

 

 

Lässt eine Stelle des Negativs 1/100 des Lichts durch, ist die eingestrahlte Menge 100 mal so groß wie die durchgelassene Lichtmenge und die Opazität 100. Der Dichtewert ergibt sich aus dem Zehnerlogarithmus von 100, also 2. Der Dichtewert D =2 sagt aus, dass nur noch 1% des Lichts durchgelassen wird.

 

D = log 1/0,01           oder

D = log 100 = 2

 

 

 

 

Bei 3 wird nur noch ein 1/1000 durchgelassen (0,1%).

Der Dynamikumfang von 3 (1000:1) ist etwas weniger als 10 LW /Blendenschritte (210 = 1024).

 

D = log 1/0,001         oder

D = log 1000 = 3

 

 

 

 

 

 

 

 

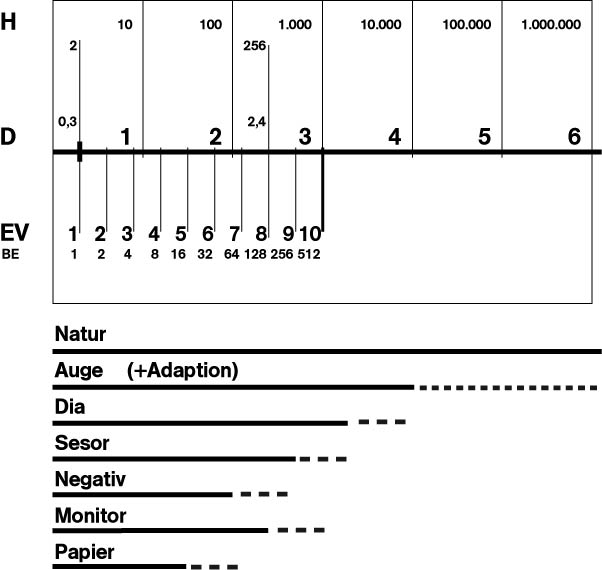
Und je nachdem wie sehr die Qualität am späteren Ausgabemedium ist (Papier, Monitor, Projektion,) kann der Kontrastumfang größer oder kleiner sein.

 

 

 

 

 

 

Kontrastumfang

 

Der Kontrastumfang beschreibt das Verhältnis zwischen hellstem Punkt und dunkelstem Schatten eines Bildes. Ein anderes Wort wäre Dynamikumfang oder Dichteumfang, die Fähigkeit zur Erfassung und Wiedergabe von Kontrasten.

 

Und damit sind wir beim Grundproblem der Fotografie angelangt.  Denn die Helligkeitsunterschiede sind in der Natur viel differenzierter als sie ein Sensor oder ein Negativ wiedergeben könnten. Das merkt man schon allein bei der brennenden Mittagssonne, wo die Helligkeitsabstufungen schon bis zu 1.000.000:1 betragen können. Der Belichtungsspielraum zwischen feinsten Wolken und tiefsten noch fein gezeichneten Kontrastdetails der Schatten würde demnach einem Dynamikumfang von 6 entsprechen.

 

Das sind rein theoretische Überlegungen, denn die maximalen Lichtwerte die in unseren Breiten bei strahlender Sonne und wolkenlosem Himmel gemacht werden können liegen bei etwa 14 Blendenstufen Motivkontrast (bei ISO 100).

 

 

 

Unser Auge kann einen Kontrastumfang von 14 Blenden leicht umfassen, anders ausgedrückt von mindestens vier Größenordnungen, in Zahlen: 10.000:1 – zehntausend unterschiedliche Helligkeitsstufen kann es wahrnehmen.

Umgerechnet auf den Dichteumfang entspricht dieser D = 4. Ebenso ein gutes Dia, das bis zu 10.000 Schwärzungsunterschiede schafft.

 

Das Auge kann sich durch eine so genannte Adaption, einer Neujustierung der Iris, binnen kürzester Zeit auf andere Lichtverhältnisse einstellen und so seinen Kontrastumfang vergrößern

Schatten fallen im Erleben weit weniger gewichtig aus als am Foto (von den minimalen Korrekturen merken wir nichts)

Deutlich wahrnehmbarer wird das Phänomen erst wenn wir vom grellen Sonnenlicht in einen abgedunkelten Raum gehen. Das Auge braucht eine gewisse Zeit zur Adaption, damit wir auch hier alle Details erkennen können

Grundsätzlich kann das Auge durch seine Fähigkeit zur Adaption einen Kontrastumfang von 1:1.000.000 also 20 Bit bewältigen

 

 

 

 

Gängige Standardsensoren einer Kamera dagegen nur 1.000:1.

Inzwischen haben die Digitalmodelle den Dynamikumfang von konventionellen Farbfilmen erreicht (Bandbreite von 9 – 11 Blendenstufen).

 

Mit hochwertigen Sensoren moderner Kameras erreicht man 1:2.000. Wenn sie die den meisten von ihnen zur Verfügung stehenden 12 Bit ausnutzen, kommen sie maximal auf einen Kontrastumfang von 1:4.096.

Zwar gibt es auch Kameras die einen 14-Bit Sensor haben (Kontrast 1:16.384), doch bleiben auch diese hinter dem menschlichen Auge zurück.

Zusammen mit einer 16-Bit Verarbeitung und Speicherung (Raw) stellt diese Technologie die bestmögliche Informationsspeicherung dar.

Intern arbeitet das Format in 16-Bit, was bedeutet, dass der Kontrastumfang höchstens bei 15 EV oder einem Dichteumfang von 4,5 liegt.

Zwar kommt es hier wieder zu einer Reduzierung der Farbnuancen, doch gleichzeitig sieht man, dass gewisse Stellen (die Lichter und Schatten) besser durchzeichnet sind.

Nur kommt diese Technik nicht an die realen Verhältnisse der Lichtverteilung der Natur heran.

 

 

 

Die Belichtungsautomatik errechnet dann einen Mittelwert und blendet kurzerhand alle Details aus, die zu Hell oder zu dunkel sind

Im Ergebnis haben die Wolken ebenso wenig Zeichnung wie die dunklen Partien des Bodens

 

Dieses Wahrnehmungsdefizit bleibt aber auf die Kamera beschränkt

Unser Auge realisiert gar nicht, dass es mehr als die Kamera erkennt und das führt dazu, dass man eventuell unangenehm überrascht ist, aufgrund unserer Erinnerung des Detailreichtums

 

 

 

 

 

 

 

Auch wenn ein Kamerasensor einen Großteil abbilden könnte, blieb das Problem der Wiedergabe

 

 

 

Ein gewöhnlicher Monitor hat dagegen nur eine Farbtiefe von 8 Bit, also 8 Blendenstufen. Das entspricht einen Dichteumfang von 2,4, also einen Dynamikumfang von als 1:255. Hochwertige Modelle erreichen bis zu 1:1.000 oder mehr.

 

Es gehen auch am Monitor viele Details verloren, die die Kamera erfasst hat (wie es in der 8-Bitumwandlung eines Jpegs der Fall ist)

 

Wird das Bild im Standardformat gespeichert, stehen ihm ein 256 unterschiedliche Helligkeitsstufen bei 8 Bit Farbtiefe zur Verfügung. Was einem Umfang von 255:1 Helligkeitsunterschieden entspricht.

Bei Raw Dateien bleibt der volle Tonwertumfang erhalten.

 

 

 

 

Wenn ein Bild auf Papier gedruckt oder ausbelichtet wird, bleibt je nach Medienqualität nur noch ein Kontrastumfang von 1:32 bis 1:100 übrig

 

Es müsste also eine einfache Kamera reichen, weil ohnehin alle Feinheiten bei der Wiedergabe am Bildschirm und Papier verloren gehen

 

 

 

Die Dichte ist ein guter Wert um Filmmaterial oder Sensor vergleichen zu können.

Beispielhafte Werte für D:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

http://www.sw-magazin.de/swmag_wollstein_04.htm

Peter Fischer-Piel  -  Das Zonensystem  -  ikoo  -  1986